AHC034 参加記 | 2024.06 | Articles

AHC034 お疲れさまでした！
最近 H レーティング全然上がらね～～～って出るの躊躇していて、問題は見るけど提出しないみたいなことが続いてしまっていました。
結果的に半年くらいぶりに参加することになりました。

その結果とても良い順位が出たので、せっかくなので記録として残したいと思います。
わかりづらい点があったら提出コードを参照してください 🙇

問題概要

$N \times N$ マスあって、各マスには初期高さが決まっている。
コストを小さくマスの高さを 0 に整地してね。
マスの初期高さの総和は 0 だよ。

やったこと

提出一覧

うーん... DP すればいいんじゃね？？

ということで DP で解きました。
上位の方々はみんな焼きなましとかビームサーチとか最小費用流している印象なので、かなり珍しい解法だったのではないかと思います。
まったくヒューリスティック的手法は用いていません。
詳細を書きます。

DP 配列を $dp[k][(x,y)]$ とします。
$k$ マスの高さを 0 としたとき・ $(x,y)$ にいるときの状態を表します。
保持しておく値は、 (コスト, ダンプカーに積まれた土砂の量, 前にいた位置, すでに 0 に整地したマスを管理する bitset) の 4 値 tuple です。
bitset は $N^2 = 400$ ビットで、 64 倍高速化されることになるので、計算量の話では無視します。

遷移としては、 $(x, y)$ から $(nx, ny)$ に移動する、 $(nx, ny)$ を 0 に整地するといった遷移です。
各マスについて中途半端な値に整地するということは考えていません。
遷移しないのは、

すでに整地した場所
高さがマイナスで、土砂の量が足りない

のケースで、それ以外の遷移できるケースなら高さを 0 に整地して、コストを加算します。
このとき、ダンプカーに積まれた土砂の量を保持しているので、マンハッタン距離を用いてコストが計算できます。
コストが最小となるように遷移を行っていきます。
$k$ の小さい順に遷移を行っているため、 $dp[k][*]$ には順番に決めていったときの各マスの最小コストが保持されることになります (たぶん)。

DP の状態数は $(N^2 + 1) \times N^2$ であり、各マスからの遷移先は $N^2$ 通り、各遷移の計算が $O(1)$ です。
全体で $O(N^6)$ です。

こうして計算した後、 $dp[N^2][*]$ の最小値を答えとします。
この解の遷移を復元して、解を得ます。

少し不安だったので bitset 高速化以外にも、 array を使うようにしたり、 $n$ の値を constexpr 化したりしました。
コードテストで試してみたところ、 100ms くらいで終了したので、これを提出しました。

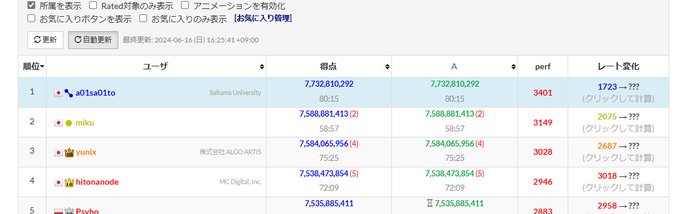
提出 #54634686: 7732810292 点

するとなんと、開始から 80 分くらい経過していたにもかかわらず、提出時点で 1 位でした！
とても想定していない結果だったので、驚いて震えていました...。

Asa

@a01sa01to

·Follow

First Sub が 1 位とかいくらなんでも面白すぎる、今終わってくれ～

16:26 · Jun 16, 2024 (GMT+9)

結果と感想

Asa

@a01sa01to

·Follow

AHC034 お疲れさまでした～ 33 位！かな？ First Sub が提出時 1 位をとってしまいびっくりでも 1 ページ目死守できず... パラメータ調整うまくやったらもうちょい点数上がったかなぁ... やったこと: † ただの DP † ヒューリスティック的なことはほぼ何もやってない...w atcoder.jp/contests/ahc03…

19:01 · Jun 16, 2024 (GMT+9)

Read 1 reply

Asa

@a01sa01to

·Follow

A/H 初の橙 perf！やった～！！ a01sa01toさんのトヨタ自動車プログラミングコンテスト2024#6（AtCoder Heuristic Contest 034）での成績：36位パフォーマンス：2403相当レーティング：1723→1873 (+150) :) Highestを更新し、1 級になりました！ #AtCoder #AHC034 atcoder.jp/users/a01sa01t…

19:33 · Jun 16, 2024 (GMT+9)